Home FPTU SecAthon 2021 | Cryptographic Writeup | CRY301
Post
Cancel

FPTU SecAthon 2021 | Cryptographic Writeup | CRY301

Posted Oct 10 6 min read

CRY301

Source code and analysis

Một bài crypto giải bằng kiến thức toán học và tư duy về code. Full source code đề bài xem tại đây

Bài này yêu cầu mình tìm được số x ban đầu từ kết quả của 2 hàm easyone(x) và alittlebitharderone(x).

Phân tích hàm easyone(x)

Nhìn sơ qua hàm easyone(x), có 3 phép biến đổi chính được lặp đi lặp lại 3 lần:

  • Phép xor với left shift bit của chính nó

  • Phép nhân

  • Phép & với 0xffffffffffffffffffffffffffffffff.

1
2
3
4
5
6
7
8
9
10
11
12
13

def easyone(x):
    assert(x < 2 ** 128)
    x ^= x >> (64 + 19)
    x *= 0xd3856e824d9c8a26aef65c0fe1cc96db #281159923981539500379670095774511568603
    x &= 0xffffffffffffffffffffffffffffffff
    x ^= x >> (64 + 3)
    x *= 0xe44035c8f8387dc11dd3dd67097007cb #303397380928069120521467215513016862667
    x &= 0xffffffffffffffffffffffffffffffff
    x ^= x >> (64 + 20)
    x *= 0xc9f54782b4f17cb68ecf11d7b378e445 #268448390289851351177030176676964262981
    x &= 0xffffffffffffffffffffffffffffffff
    x ^= x >> (64 + 2)
    return x

Như vậy, có 2 bài toán đặt ra cần giải quyết:

  • Tìm x biết a * x = b (mod n) với a, b, n đã cho trước

  • Khôi phục lại kết quả phép xor. Tìm x có $a \oplus x = b$ với a, b đã biết, khá đơn giản với $x = a \oplus b$.

Cùng đi sâu hơn chút vào từng bài toán 1 nhé

Bài toán đầu tiên

Đây là bài toán cơ bản cơ bản về inverse mod (modular inverse) trong finite field (trường hữu hạn). Đơn giản, mình có thể tìm $x$ bằng cách $x = a^{-1} * b$ $(mod$ $n)$, trong đó, $a^{-1} * b$ $(mod$ $n)$ là giá trị inverse modulo của a trong finite field $(mod$ $n)$

Chi tiết cách tìm inverse mod bằng toán học với extended euclidean algorithm có thể xem tại đây. Lúc code giải thì mình dùng luôn hàm invert(a, n) trong thư viện gmpy2 của python để tìm $a^{-1} * b$ $(mod$ $n)$.

Mình chuyển 1 đoạn code sang dạng bài toán gốc để dễ hình dung. Cụ thể, đoạn code dưới đây biểu diễn dưới dạng toán học sẽ là $x * 281159923981539500379670095774511568603 = b$ $(mod$ $n)$ với b có thể thu được từ việc dịch lại phép xor (bài toán 2).

Lưu ý: x &= 0xffffffffffffffffffffffffffffffff <=> x %= 0xffffffffffffffffffffffffffffffff hay x %= 2**128

1
2

x *= 0xd3856e824d9c8a26aef65c0fe1cc96db #281159923981539500379670095774511568603
x &= 0xffffffffffffffffffffffffffffffff

Như vậy, ta có thể dễ dàng tìm x với $x = b$ $∗$ $281159923981539500379670095774511568603^{−1}$ $(mod$ $2^{128})$

1
2

x *= gmpy2.invert(268448390289851351177030176676964262981, 2**128)
x &= 0xffffffffffffffffffffffffffffffff

Vấn đề là để hoàn thiện quá trình giải thì mình cần tìm b, nghĩa là cần phải giải quyết bài toán số 2.

Bài toán thứ 2

Để giải quyết phần xor này, chúng ta cần phải lưu tâm x sau khi bitshift thì còn những bit nào còn giữ nguyên, bit nào dịch chuyển để thực hiện xor.

1

x ^= x >> (64 + 2)

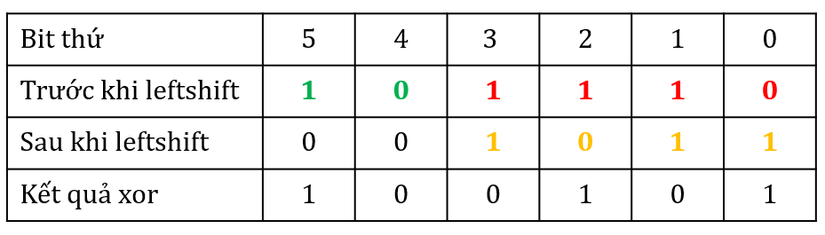
Để dễ hình dung, bạn có thể nhìn hình mô phỏng trước và sau khi leftshift dưới đây. Bit màu xanh là những bit còn giữ nguyên sau khi leftshift. Bit màu vàng là bit màu xanh được chuyển ra sau khi leftshift. Bit màu đỏ là những bit có thể bị thay đổi sau bitshift (và cũng là bit thực sự tham gia xor)

1

Dễ dàng nhận thấy, phần bit dùng để xor với giá trị x ban đầu vẫn giữ nguyên sau khi xor $\longrightarrow$. Như vậy mình có thể dễ dàng khôi phục phần bit dùng để xor bằng cách leftshift lại giá trị sau khi xor bằng đúng một khoảng dùng để xor trước đó (tức leftshift (64 + 2) đơn vị trong trường hợp trên).

Kết luận trên đúng với tất cả trường mà x được leftshift ít nhất 64 đơn vị.

Vậy là mình đã giải quyết xong cả 2 bài toán trên! Cuối cùng mình có đoạn code để lấy giá trị x từ hàm easyone(x) như sau:

1
2
3
4
5
6
7
8
9
10
11
12

def solveeasyone(x):
    x ^= x >> (64 + 2)
    x *= gmpy2.invert(268448390289851351177030176676964262981, 2**128)
    x &= 0xffffffffffffffffffffffffffffffff
    x ^= x >> (64 + 20)
    x *= gmpy2.invert(303397380928069120521467215513016862667, 2**128)
    x &= 0xffffffffffffffffffffffffffffffff
    x ^= x >> (64 + 3)
    x *= gmpy2.invert(281159923981539500379670095774511568603, 2**128)
    x &= 0xffffffffffffffffffffffffffffffff
    x ^= x >> (64 + 19)
    return int(x)

Tada, first round~~

2

Phân tích hàm alittlebitharderone(x)

Giải quyết hàm này cũng cần giải quyết 2 bài toán như hàm easyone(x). Bài toán 1 về tìm inverse mod hoàn toàn giống hệt. Cái khó hơn nằm ở Bài toán 2, do mình không thể ngay lập tức khôi phụ được bit dùng trong phép xor trước đó từ kết quả thu được.

Tuy nhiên, điều đáng mừng là nguyên lý cách làm vẫn thế. Chúng ta cũng sẽ dùng những bit còn nguyên, để khôi phục lại những bit gốc, rồi lân la dần dần để khôi phục toàn bộ bit gốc đó. Mình mô phỏng với 1 bài toán nhỏ với 1 chuỗi 6 bit với độ leftshift bằng 2 như sau:

3

Với trường hợp như trên, mình khôi phục lại giá trị ban đầu của x bằng cách đi qua từng bước như sau đây (Mô tả bằng hình ảnh cho dễ hiểu nhé)

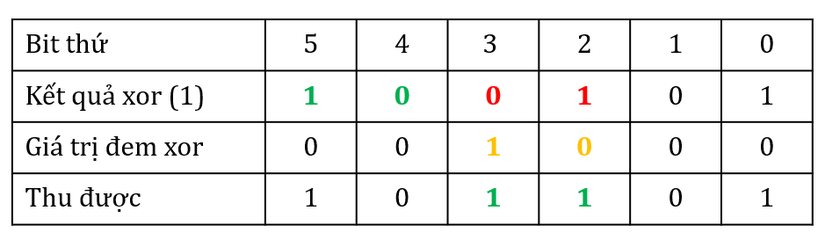
  • Xor 2 bit đầu (2 bit còn giữ nguyên sau khi xor) với 2 bit liền kều sau nó. Những bit còn lại giữ nguyên. Như vậy, mình đã khôi phục lại được bit số 3 và bit số 2:

    4

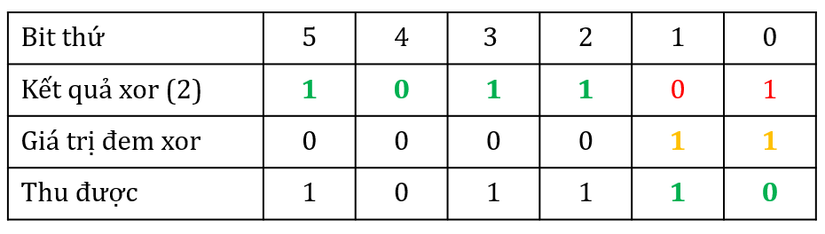
  • Xor tiếp 2 bit vừa thu được (bit số 3 và 2) với 2 bit liền kề sau nó để khôi phục tiếp 2 bit còn lại (bit 5 và 6) : 5

Vậy làm mình đã thu lại được đoạn bit gốc, tức giá trị của x cần tìm. Với chuỗi bit dài hơn, mình chỉ cần chạy quá trình trên lặp đi lặp lại là được.

Dễ rồi phải không? Mặc dù mình nghĩ ra được ý tưởng mình việc code tốn của mình tận 30 phút… và cuối cùng lại chỉ thành 1 đoạn code ngắn ngủi sau:

1
2
3
4
5
6
7
8

def xor(a, b):
    return ''.join(str(int(_a) ^ int(_b)) for _a, _b in zip(a, b))

def shiftsolong(x, bitshift):
    x = '{0:b}'.format(x)
    for i in range(0, len(x) - bitshift):
        x = x[:bitshift*(i+1)] + xor(x[bitshift*i:bitshift*(i+1)], x[bitshift*(i+1):bitshift*(i+2)]) + x[bitshift*(i+2):]
    return int(x, 2)

Ta nói đời về căn bản là buồn mà 😢 Thôi tổng hợp lại, thì mình có đoạn code lấy lại giá trị x từ hàm alittlebitharderone(x):

1
2
3
4
5
6
7
8
9
10
11
12

def solvehardone(x):
    x = shiftsolong(x, 2)
    x *= gmpy2.invert(268448390289851351177030176676964262981, 2**128)
    x &= 0xffffffffffffffffffffffffffffffff
    x = shiftsolong(x, 20)
    x *= gmpy2.invert(303397380928069120521467215513016862667, 2**128)
    x &= 0xffffffffffffffffffffffffffffffff
    x = shiftsolong(x, 3)
    x *= gmpy2.invert(281159923981539500379670095774511568603, 2**128)
    x &= 0xffffffffffffffffffffffffffffffff
    x = shiftsolong(x, 19)
    return int(x)

Qua vòng 2 và nhận được flag. Chỉ là không kịp submit nữa…

6

Nếu có ước muốn trong cuộc đời này, mình sẽ ước có một không gian riêng mà thời gian chảy chậm để ngồi debug trước khi hết giờ FUSEC 😇

CTF, Cryptographic Challenges
writeups cryptographic fusec21
This post is licensed under CC BY 4.0 by the author.

Recent Update

Contents